深度学习
深度前馈网络
一种经典的神经网络结构,这种网络通常由多层神经元组成,层与层之间是单向传递信号的结构,因此称为“前馈”,意味着信息从输入层流向输出层,不会存在反馈连接。典型的深度前馈神经网络包括输入层、若干隐藏层和输出层。每个神经元会接收来自前一层神经元的输入,将其进行加权求和并通过激活函数处理后输出给下一层
网络架构的建立、损失函数的选择、输出单元和隐藏单元的设计、训练误差的处理等问题是深度前馈网络设计中的一系列核心问题
自编码器
自编码器是包含若干隐藏层的深度前馈神经网络,其独特之处是输入层和输出层的单元数目相等
将编码映射记作 ϕ,解码映射记作 ψ,自编码器的作用就是将输入 X 改写为 (ψ∘ϕ)(X)
如果以均方误差作为网络训练中的损失函数,自编码器的目的就是找到使均方误差最小的编解码映射的组合
$$ \phi,\psi=\arg\min_{\phi,\psi}||\mathbf{X}-(\phi\circ\psi)(\mathbf{X})||^2 $$
从信息论的角度看,编码映射可以看成是对输入信源 X 的有损压缩,学习的作用就是习得在训练数据集上更加精确的映射,并希望这样的映射在测试数据上同样表现良好,也就是使自编码器具有较好的泛化性能
优化
优化问题:
- 病态矩阵:数值精度导致的不可避免的舍入误差可能会给输出带来巨大的偏离,病态矩阵对输入的敏感性会导致很小的更新步长也会增加代价函数,使学习的速度变得异常缓
- 局部极小值:在神经网络,尤其是深度模型中,代价函数甚至会具有不可列无限多个局部极小值,这显然会妨碍对全局最小值的寻找
- 鞍点:梯度为 0 的临界点,但它既不是极大值也不是极小值
随机梯度下降法(stochastic gradient descent)就是在传统机器学习和深度神经网络中都能发挥作用的经典算法,就是每走一步就换个方向。为了节省每次迭代的计算成本,随机梯度下降在每一次迭代中都使用训练数据集的一个较小子集来求解梯度的均值
随机梯度下降会受到噪声的影响。当学习率固定时,噪声会阻止算法的收敛;而当学习率逐渐衰减时,噪声也会将收敛速度压低到次线性水平,降噪的方法有动态采样、梯度聚合和迭代平均三类。为了提升梯度下降的性能,可以通过使用二阶导数近似方法
除此之外,还有动量方法(momentum)、加速下降方法(accelerated gradient descent)和坐标下降方法(coordinate descent)等方法来进行改进梯度下降
神经网络
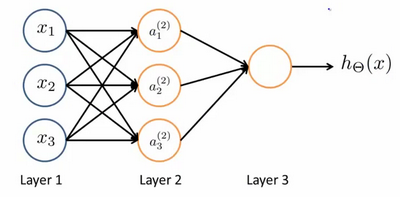
layer1 是输入层,每个节点就是一个特征值
layer2 是隐藏层,每个节点是一个逻辑回归神经元,每个神经元接收上一层的1个或多个特征,产生一个新特征,输出给下一层,接收特征的输入被称为激活,接收特征的输入被称为激活函数,逻辑回归神经元的激活函数是sigmoid函数
layer3 是输出层,其根据上一层输出的所有特征,再输出一个特征值
从左向右每个特征被计算成新特征,这个过程称之为前向传播,Tensorflow使用反向传播算法来替代梯度下降计算出参数
隐藏层中每个神经元处理数据的方式,计算什么特征,都是根据训练数据统计所决定的,而非人工指定
神经网络每一层输出的特征值都比上一层的特征更高级,所以也就能更好地预测数据
# 手动实现前向传播过程
x = np.array([220,200,17])
# 第一层第一个神经元
w1_1 = np.array([1,2])
b1_1 = np.array([-1])
z1_1 = np.dot(w1_1, x) + b1_1
a1_1 = sigmoid(z1_1)
# 第一层第二个神经元
w1_2 = np.array([-3,4])
b1_2 = np.array([-1])
z1_2 = np.dot(w1_2, x) + b1_2
a1_2 = sigmoid(z1_2)
# 第一层第三个神经元
w1_3 = np.array([5,-6])
b1_3 = np.array([-1])
z1_3 = np.dot(w1_3, x) + b1_3
a1_3 = sigmoid(z1_3)
# 第二层
w2_1 = np.array([-7,8,9])
b2_1 = np.array([3])
z2_1 = np.dot(w2_1,a1)+b2_1
a2_1 = sigmoid(z2_1)
结果 = a2_1
激活函数
如果没有激活函数,也就是使用线性激活函数,那么整个神经网络就跟线性回归一样,解决不了更复杂的问题
不同的激活函数会导致神经元输出的模式也不一样
- sigmoid
- 线性激活函数:输入什么就输出什么,等于没有激活函数
- ReLu: 小于0输出0,大于0,输出输入本身
对于输出层,如果解决的是二分类问题,那就需要使用sigmoid,如果解决的是回归问题,输出有负数,选择线性激活函数,输出没有负数,选择ReLu
对于隐藏层,大多数情况下使用的都是ReLu,因为它梯度下降比sigmoid更快
优化算法
- Adam:相比传统的梯度下降算法,这种优化算法使得学习率$a$不是固定的,而是会根据运行情况调大会调小以优化性能
卷积层
卷积层的每个神经单元不会接受上一层的全部特征输入,而是有选择的选择一部分特征,不同神经元选择的特征集合会重叠
可以通过不同的核函数来提取不同的特征
卷积神经网络
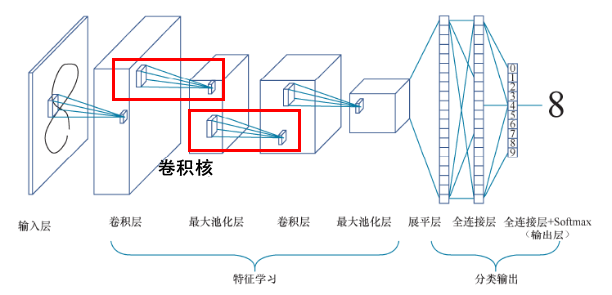
一个卷积神经网络的工作流程:
输入层将待处理的图像转化为一个或者多个像素矩阵,卷积层利用一个或多个卷积核从像素矩阵中提取特征,得到的特征映射经过非线性函数处理后被送入池化层,由池化层执行降维操作。卷积层和池化层的交替使用可以使卷积神经网络提取出不同层次上的图像特征。最后得到的特征作为全连接层的输入,由全连接层的分类器输出分类结果
深度信念网络
一种概率生成模型,能够建立输入数据和输出类别的联合概率分布
深度信念网络可以看成由若干简单的学习单元构成的整体,而构成它的基本单元就是受限玻尔兹曼机,受限玻尔兹曼机的模型非常简单,就是一个两层的神经网络,包括一个可见层和一个隐藏层
感知机模型
一种二分类的监督学习算法,能够决定由向量表示的输入是否属于某个特定类别
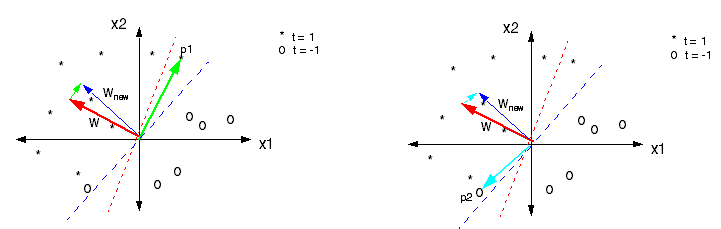
- 初始化权重 $w(0)$ 和阈值,其中权重可以初始化为 0 或较小的随机数
- 对训练集中的第 $j$ 个样本,将其输入向量 $x_j$ 送入已初始化的感知器,得到输出 $y_j(t)$
- 根据 $y_j(t)$ 和样本 $j$ 的给定输出结果 $d_j$,按以下规则更新权重向量
$$ w_i(t+1)=w_i(t)+\eta[d_j-y_j(t)]\cdot x_{j,i} $$
即找出合适的 $W$ 使得训练样本的预测值与实际值的差别最小
感知机以所有误分类点到超平面的总距离作为损失函数,用随机梯度下降法不断使损失函数下降,直到得到正确的分类结果
径向基神经网络
包含三层:一个输入层、一个隐藏层和一个输出层。其中隐藏层是径向基网络的核心结构
每个隐藏神经元都选择径向基函数作为传递函数
训练过程:
- 通过一些方法选择隐藏层中的中心点。常见的方法包括使用样本数据的子集或者通过聚类算法确定中心点
- 对于每个径向基函数,需要确定其宽度参数,决定了径向基函数在输入空间中的影响范围
- 对于每个样本,计算其与每个中心点的距离,并将距离作为径向基函数的输入,得到隐藏层的输出
- 输出层训练:使用类似于其他神经网络的方法,通过反向传播算法来调整输出层的权重,以最小化训练误差
自组织特征映射
能够将高维的输入数据映射到低维空间之上(通常是二维空间),采用的是竞争性学习
自组织映射的结构是,一张一维或者二维的网格,网格中的每个节点都代表一个神经元,神经元的权重系数则是和输入数据的维度相同的向量,距离较近的神经元能够处理模式相似的数据,训练过程就是在空间上对神经元进行有序排列的过程
模糊神经网络
将常规的神经网络赋予模糊输入信号和模糊权值,其作用在于利用神经网络结构来实现模糊逻辑推理
构成模糊神经网络的基本单元是模糊化的神经元。模糊神经元的输入信号和权重系数都是模糊数,传递函数也需要对模糊集合上的加权结果进行处理,模糊数就是只有取值范围而没有精确数值的数
为了训练网络,如果保持学习率参数不变,误差函数就难以快速收敛。即使收敛也可能陷入局部最小值上,在不同的学习率参数下得到不同的局部最小值。为了处理这个问题,模糊神经网络引入了一种叫做共轭梯度(conjugate gradient)的机制
循环神经网络
引入了时间的维度,因而适用于处理时间序列类型的数据
$$ \mathbf{h}_t=f(\mathbf{W}\mathbf{x}t+\mathbf{U}\mathbf{h}{t-1}) $$
当前时刻的状态与先前的状态有关
普通的循环神经网络中,记忆只会涉及到过去的状态。如果想让循环神经网络利用来自未来的信息,就要让当前的状态和以后时刻的状态同样建立起联系,得到的就是双向循环神经网络
递归神经网络
循环神经网络的特点是在时间维度上共享参数,从而展开处理序列。如果换一种展开方式,将序列数据展开成树状结构,用到的就是递归神经网络
生成式对抗网络
- 生成器(generator):从随机噪声中模拟真实数据样本的潜在分布
- 判别器(discriminator):判断输入是真实数据还是模拟的数据
对网络的训练就是让判别器区分真实数据和伪造数据的准确率最大化,让生成器生成的数据被判别器发现的概率最小化
$$ \arg\min_g\max_D-\dfrac12\int_x[p_{aata}(x)\log(D(x))+p_g(x)\log(1-D(x))]\mathrm{d}x $$
长短期记忆网络
长短期记忆的基本单元的作用在需要时取出并聚焦记忆,通常包括四个功能不同的隐藏层:记忆模块(memory cell)、输入门(input gate)、输出门(output gate)和遗忘门(forget gate)
首先,遗忘门根据当前输入和前一步隐藏状态,决定哪些信息要从细胞状态中遗忘。
然后,输入门根据当前输入和前一步隐藏状态,确定更新细胞状态的新信息,并结合遗忘门的结果更新细胞状态。
最后,输出门根据当前的细胞状态和输入,计算并输出当前时刻的隐藏状态
表示学习
学习数据的有用特征,使得这些特征能够更好地捕捉数据的结构和模式